Ахмадалиев Ғайратжон Нематиллаевичнинг
фалсафа доктори (PhD) диссертацияси ҳимояси ҳақида эълон

 
I. Умумий маълумотлар.
Диссертация мавзуси, ихтисослик шифри (илмий даража бериладиган фан тармоғи): “Гиперболик функсияларга аниқ бўлган тақрибий интеграллаш формулаларини оптималлаштириш”, 01.01.03–Ҳисоблаш математикаси ва дискрет математика (физика-математика фанлари).
Диссертация мавзуси рўйхатга олинган рақам: В2021.2.PhD/FM603.
Илмий раҳбар: Шадиметов Холматвай  Махкамбаевич, физика-математика фанлари доктори, профессор.
Диссертация бажарилган муассаса номи: Тошкент давлат транспорт университети.
ИК фаолият кўрсатаётган муассаса номи, ИК рақами: Ўзбекистон Миллий университети ҳузуридаги ДСc.03/30.12.2019.ФМ.01.02 рақамли илмий кенгаш.
Расмий оппонентлар: Нормуродов Чори Бегалиевич, физика-математика фанлари доктори, профессор; Нуралиев Фарход Абдуғаниевич, физика-математика фанлари доктори, доцент.
Етакчи ташкилот: Қорақалпоқ давлат университети
Диссертация йўналиши: назарий ва амалий аҳамиятга молик.
II. Тадқиқотнинг мақсади. Гилберт фазоларида оптимал квадратур формулаларни қуриш алгоритмини ишлаб чиқиш ва оптимал алгебраик-гиперболик квадратур формулаларни қуриш учун уни амалга оширишдан иборат.
III. Тадқиқотнинг илмий янгилиги қуйидагилардан иборат:
умумий ҳолда 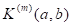  гилберт фазосида Соболев методи ёрдамида вазнли оптимал квадратур формулаларни қуриш алгоритми ишлаб чиқилган;
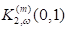  фазода ишлаб чиқилган алгоритм алгебраик кўпҳадлар ва гиперболик функсияларга аниқ бўлган оптимал квадратур формулаларни қуриш учун қўлланилган;
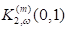  фазодаги алгебраик-гиперболик квадратур формулаларнинг хатолик функсионали нормаси квадратининг ифодасини экстремал функсия тушунчасидан фойдаланиб топилган;
оптимал алгебраик-гиперболик квадратур формулаларнинг коеффициентлари учун Лагранж аниқмас кўпайтувчилар методи ёрдамида чизиқли алгебраик тенгламалар системаси олинган ҳамда унинг ечимини мавжудлиги ва ягоналиги мос бир жинсли системанинг фақатгина тривиал ечимга эга эканлиги асосида исботланган;
Грин функсиясига мос келувчи дискрет бороно шаклдаги функсияга Фуре алмаштиришини қўллаш ёрдамида ушбу   дифференциал операторнинг дискрет аналоги қурилган;
оптимал коеффициентлари учун олинган системани ўрамали тенгламага келтириб дискрет оператор ёрдамида оптимал алгебраик-гиперболик квадратур формуланинг коеффициентлари топилган.
IV. Тадқиқот натижаларининг жорий қилиниши: Оптимал алгебраик-гиперболик квадратур формулаларни қуриш ва уларнинг гилберт фазосида хатоликларини баҳолашда олинган натижаларга асосланиб:
ихтиёрий 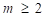  учун 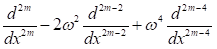   операторнинг қурилган дискрет аналогидан ОТ-Атех-2018-340-“Икки тезликли муҳит динамикасининг амалий геофизик масалаларини назарий ва сонли тадбиқ этиш” мавзусидаги давлат илмий-техник дастурлари амалий лойиҳасида фойдаланилган (Қарши давлат университетининг 2024 йил 28-июндаги 04/1883 сонли маълумотномаси). Натижада ёпишқоқ – эластик тенгламалар системасида диагонал матрицали ядрони аниқлаш масаласининг ягоналик ва турғунлик баҳолари мавжудлигини ўрганиш имконини берган.
диссертациясида олинган илмий натижалардан 2018-2020 йилларда бажарилган ФА-Атех-2018-414 рақамли “Бойитиш комбинатларида энергия сарфини пасайтирувчи чиқинди маҳсулотлари гидротранспорт технологиясини ишлаб чиқиш” мавзусидаги амалий лойиҳани бажаришда ушбу диссертация натижаларидан фойдаланилган (Механика ва иншоотлар сейсмик мустаҳкамлиги институтининг 2024 йил 06-сентябрдаги 9983 сонли маълумотномаси). Натижада диссертацияда реакция-диффузия типидаги параболик тенгламалар системаси учун номаълум чегарали масалалар  ечимлари илмий натижаларидан фойдаланиш, кон-металлургия комбинатларида кўп фазали муҳитларни қувурлар орқали оқими турли мураккаб физик, механик жараёнлар қонуниятларини ифодалашда, маълум хусусий ҳосилали дифференциал тенгламаларни ечишда, янги оптимал алгоритмлар қуриш усуллари ва хоссаларидан муҳим натижалар олиш имконини берган.